Loose Octrees

November 14, 2008

Graphics

approximately 2 minutes to read

As wished by one of my fellow readers, here’s an article about loose octrees. A loose octree is an adaptive spatial subdivision approach, which is very easy to implement and gives pretty good performance.

Basics

Usually, an octree subdivides the scene recursively into increasingly smaller cells. Let’s take a look at this in 2D:

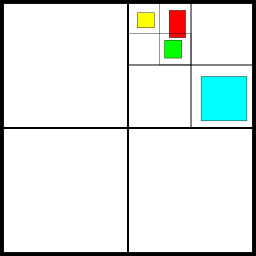
As you can see, it subdivides where the geometry is. Note that in a normal octree, the object which is slightly larger than a cell would either:

end up in the parent cell
be put into the two cells it overlaps

This is not really a problem, but it can be easily worked around by relaxing the bounds slightly. This is already the main idea behind the loose octrees: You relax the bounds to be twice the size of the object. Then, you only sort in by the centre of the bounding box, so one object always ends up in a single cell.

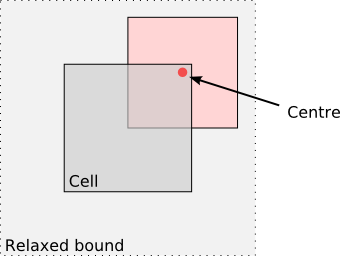
Here you can see a single cell of the octree, with its corresponding loose bound.

The loose bound is exactly twice as large as the cell itself. This gives us an important property: If we have an object which is no larger then the cell itself, and its centre is inside the cell, we can guarantee that the object is inside the loose bounds. Sorting in means that we just need to check the size, and the centre, instead of checking for overlap as we would have to do with general octrees. The only difficulty that arises is querying this tree, as we have to check against the relaxed bounds now.

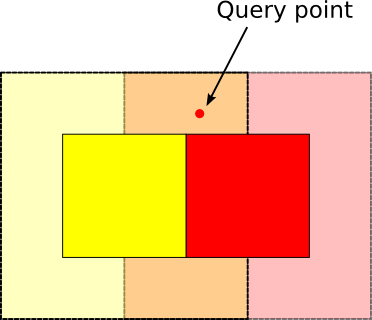
loose-query — Here you see two cells (red and yellow) with their loose bounds.

For the query point, we have to check both cells, as the point lies inside the relaxed bounds of both cells. That’s it basically.

Implementation notes

Some implementation notes:

You can store the whole tree in an array, instead of storing 8 pointers per node. Just store an offset into the array, and per node you store only:
- Object list
- Bounds
- Offset
- Pointer to the array structure (can be derived from the offset, if you can guarantee that the array starts right after your control structure)
This gives you a very tight storage structure.
Checking for the object size: If your octree is a perfect cube, you can just check the length of the diagonal. ~~In other cases, I’m currently using a dot product of the object diagonal onto the cell diagonal, and comparing this seems to work great so far for non-cube-shaped octrees.~~ For non-cube-shaped octrees, just compute the half-sized bounding box and check whether the object fits. If it is axis aligned, this is very easy.
You need to bound the scene before starting. That’s no big deal, as you can easily prune the top levels, as long as a node has exactly one child, you can use that child as the new root.

References

I didn’t invent this on my own, but rather based it on “Spatial partitioning with ‘Loose Octrees’” by Tatcher Ulrich, which you can find on his web site: http://www.tulrich.com/geekstuff/partitioning.html. I’m pretty sure this is the original source of this idea.